パーティクルフィルタの力学系への適用

最近統計数理研究所の樋口先生によって本が出版され、また実用的な観点からデータ同化への注目が高まっています。
「データ同化入門」では時間が経つごとに得られるデータを順次取り入れて予測に用いていく逐次データ同化という手法が主に紹介されています。

データ同化とカルマンフィルタ、パーティクルフィルタについてTokyoRで発表させていただきました。発表資料は以下になります。

Data assim r from xiangze

資料にも記載したようにパーティクルフィルタはシステムが非線形な方程式に従って変化する場合、システムノイズ、観測ノイズが非ガウシアンの場合にも使用できるという利点があります。
しかしながら粒子数が少なければ事前確率分布の近似も粗いものとなってしまうので真の時系列に収束しない場合もあり得ます。

実験

代表的な例として樋口先生の「データ同化入門」でも取り上げられているLorenz系をみてみます。
Lorenz系
$\dot{x}=-\sigma(x-y)$
$\dot{y}=(r-z)x-y$
$\dot{z}=xy-bz$
はパラメータrの値に応じてアトラクタが固定点、ストレンジアトラクタ、リミットサイクルと変化します。
(r>330でリミットサイクルになるのですが、その座標値は大きなものになってしまいます。)

実際のデータ同化処理では観測されたデータからある物理法則に従った隠れた変数値を推測するのですが、ここではシミュレーションを物理現象の代わりとして元のデータを生成し、その結果から一定間隔で観測ノイズを付与した上で観測値を選び出し、そこからパーティクルフィルタで元のデータを推測する手法で試しています(双子実験)。

N=100,シミュレーションの時間刻みdt=0.01
観測値を取得する間隔を1とする場合の結果が以下のようになります。
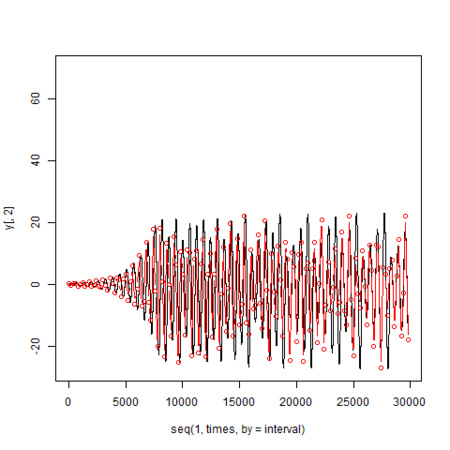
r=4(固定点)の場合
元のデータ(黒)と観測値(赤)

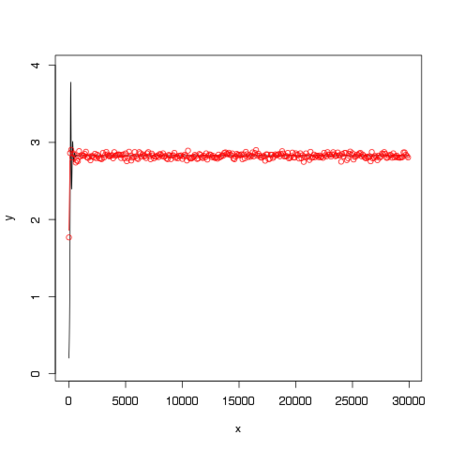
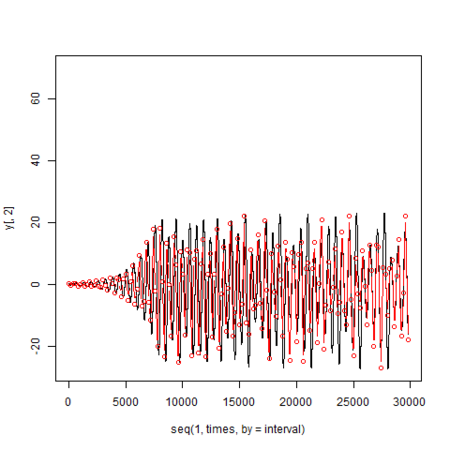
particle(黒)と観測値(赤)

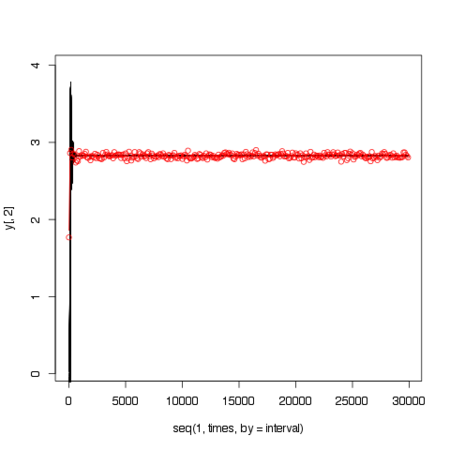
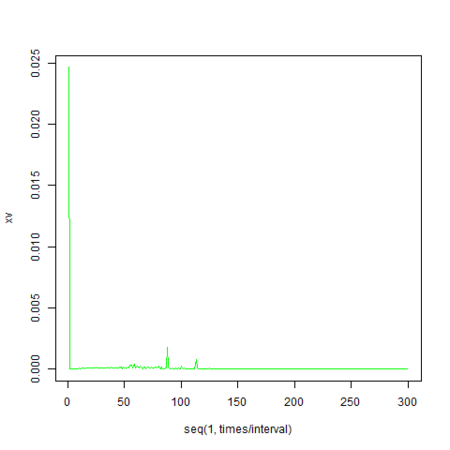
particleの座標値の分散

r=28(ストレンジアトラクタ)の場合
元のデータ(黒)と観測値(赤)

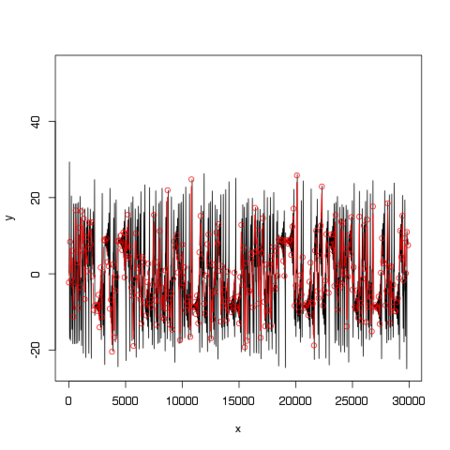
particle(黒)と観測値(赤)

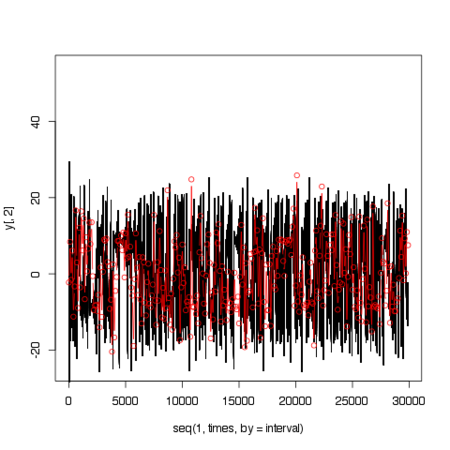
particleの座標値の分散

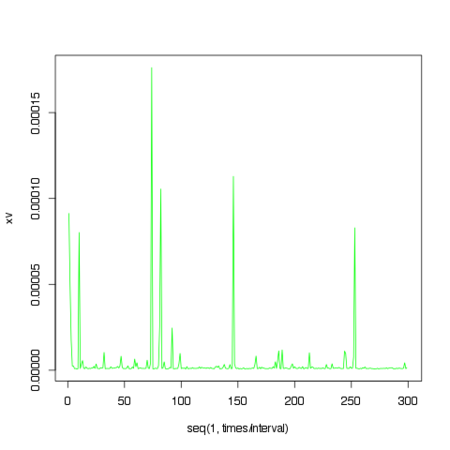
ストレンジアトラクタの場合では時たま座標値の分散が非常に大きくなってしまっています。カオス力学系のもつ軌道の不安定性が各パーティクルをばらけさせているものと考えられます。
「データ同化入門」では退化と呼ばれる粒子が状態空間内の一点に集まってしまいそれ以上発展しない退化と呼ばれる現象を防ぐ方法として融合粒子フィルタが紹介されています。ここでみられた現象と退化との関係に関しては更なる解析が必要です。

観測値の取得間隔が大きいと当然、時系列を予測する精度は悪くなります。
使用するモデルを人工的に作られたRossler方程式
$\dot{x} = -y -z$
$\dot{y} = x+ay$
$\dot{z} = b+ z(x-c)$
(a=0.1,b=0.1,c=18)
にした場合の例が以下になります。

間隔1の場合の時系列

particleの分散

間隔2の場合の時系列

particleの分散

間隔3の場合の時系列

particleの分散

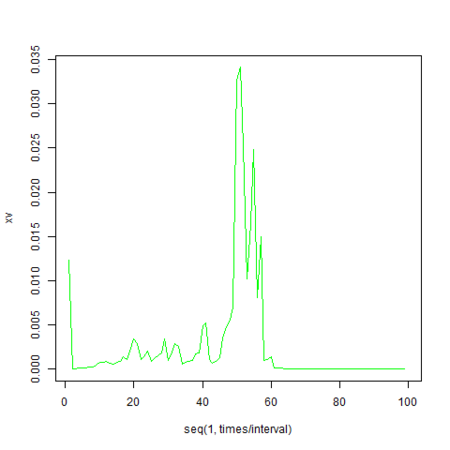
予測と実際の値とのずれが観測値の取得間隔とともに増大しますが、アトラクタの形状に起因してその傾向は時間的に変化するようです。

ソースコード

https://github.com/xiangze/particlefilter_dynamical
３次元行列を使用し、applyを使っていない部分があるのであまりきれいではありません。
平滑化処理を実装する予定です。

Reference

逐次データ同化手法としてのカルマンフィルタ、パーティクルフィルタの数式の導出が詳しく書かれています。
融合粒子フィルタの手法に関して1章が割かれ、また重点サンプリングについても解説があります。
海底地形を推測した上での津波のシミュレーション、エルニーニョの予測に用いられる大気海洋結合モデル、地球磁気圏内の荷電粒子の分布予測、遺伝子発現ネットワークのデータ同化など重要な応用が紹介されています。

データ同化入門 (予測と発見の科学)

作者: 樋口知之
出版社/メーカー: 朝倉書店
発売日: 2011/09/15
メディア: 単行本
購入: 2人クリック: 8回
この商品を含むブログ (1件) を見る

パーティクルフィルターに絞って処理の流れが丁寧に解説されています。ロボットの現在位置推定の事例も紹介されています。

予測にいかす統計モデリングの基本―ベイズ統計入門から応用まで (KS理工学専門書)

作者: 樋口知之
出版社/メーカー: 講談社
発売日: 2011/04/07
メディア: 単行本（ソフトカバー）
購入: 9人クリック: 180回
この商品を含むブログ (8件) を見る

TokyoRではBUGS言語で隠れマルコフモデル(ここでは状態空間モデル)を実装するのは難しいのではないかと口走ってしまいましたが、
Rのパッケージrjagsを用いれば
http://ito-hi.blog.so-net.ne.jp/2010-01-13
にあるような方法で可能なようです。RcppBUGS,R2WinBUGSなどでもできるかもしれません。
RcppSMCに関する@teramonagiさんの解説
３種類のモデルの違いを特にちゃんと理解したいです。
パーティクルフィルタは画像内の物体のtrackingに多く使われます。実装も比較的簡単(自分にとってはそうではなかった)らしいので独自に書かれている人もいて参考になります。ほとんどの場合モデルは等速直線運動が使われます。
OpenCVではcondensationと言う名前で機能が実装されていますが、C++のインターフェースはまだないようで少し不便です。
http://d.hatena.ne.jp/Hiroki28/20111212/1323700193
Pythonでの実装例わかりやすく、参考になります。