Group Equivariant CNNとM理論について
画像内の物体が回転したり変形したりしていても認識できるような方法に関する研究の論文を読みました。
CNNでは学習データを大量に用意しなければならず、そのために既存の画像に並行や回転などの操作を施して学習を行うと精度が向上することが知られています(data augumentation)。データを多くすることなく同程度の精度を達成するような回路構成が考えられてられてます。
Group Equivariant Convolutional Networks
https://arxiv.org/abs/1602.07576
解説
画像Iを座標x,y∈Z^2の関数として表現すると
畳み込み演算(convolution)は関数fに対する演算
として書くことができます。普通のフィルターは平行移動、回転に大して不変であり、
とかくこともできます。平行移動の処理をL:y->x-y と書くと
と書けます。
convolution *に対して
[f *ψ^i ](x) = Σ y∈G Σ K_l k=1 f_k(y)ψ^i_k(y-x)
correlation
というのが定義されています*1。ψ^i_kの中の符号が逆になっていて座標yの変換L_t: y->y+t に対してconvと逆に
となります(8)。
引数xは直接変換には出てこないことから式(11)のように座標と同様に群作用uに関しても
と書くことができます。
この方法の核心はデータxに関する変換を関数fに対する変換にすることで、これによってデータに対する変換(data augumentation)をすることなく群で表されるような変形に対して頑健な学習器を作ることが出来ます。
この論文ではCNNはconvolution, nonlinearlity,pooling によって構成されているとしています。それぞれの処理が群Gに所属する変換と可換であることを数式で示しています(6章)。
実装
(11)を実装すれば良くt,s in Gに対して(18)の加算
を計算します。Σ_h∈Gのところが既存のCNNとの違いになります。論文の主張"Computing the G-convolution for involves nothing more than indexing arithmetic and inner products, so it can be implemented straightforwardly."の通りでcorrelationの計算ではs,tに対する総和を取っています。
https://github.com/tscohen/GrouPy
主にchainerで書かれていて、tensorflowの実装もあるそうです。GPUで計算するカーネルの部分をcupyで書いているらしいです。
https://github.com/tscohen/GrouPy/blob/master/groupy/gconv/chainer_gconv/transform_filter.py#L47
index_group_func_kernel(input=w,T=self.T,U=self.U,V=self.V,output=rotated_w)
https://github.com/tscohen/GrouPy/blob/master/groupy/gconv/chainer_gconv/kernels/integer_indexing_cuda_kernel.py#L31
評価
2つの離散群p4(90度ごとの回転)とp4m(p4に鏡映を加えたもの)の実装に対してMNISTとCIFAR10
https://www.cs.toronto.edu/~kriz/cifar.html
を使い 群の要素の分和を取る分1層分での計算量は増えてしまうもののフィルターの
サイズを小さくして全体としては少ないパラメータ数で比較対象のCNNと
同程度のエラーに抑えているそうです(Table1,Table2)。
Harmonic Networks
http://visual.cs.ucl.ac.uk/pubs/harmonicNets/index.html
https://arxiv.org/abs/1612.04642
https://github.com/deworrall92/harmonicConvolutions
Group Equivariant Convolutional Networksが離散的な変換の群に対するものであったのに対して
こちらは連続的な回転群に対しても使える方法として提案されています。
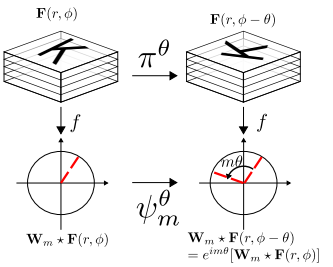
実際のところ連続群の要素を離散的にサンプリングしたものの総和を取っているようです(Figure5, Figure6)。
回転の操作を複素数で表現しています(式(5),(8),(9))。
実装
tensorflowのtf.nn.conv2d(あるいはtf.map)でcross-correlationが実装することが
できます。
def conv2d_flipkernel(x, k, name=None):
return tf.nn.conv2d(x, k, name=name, strides=(1, 1, 1, 1), padding='SAME')
https://github.com/TheAbhiKumar/tensorflow-value-iteration-networks/issues/2
https://www.tensorflow.org/versions/r0.12/api_docs/python/nn/convolution
M理論とは
https://en.wikipedia.org/wiki/M-Theory_(learning_framework)
脳内の物体認識において回転や平行移動などの変換に対する不変性は
hard codingされていない、あるいは学習によって変換に対して不変な形状が
低次元の特徴空間に埋め込めることが出来るというのが主張です。
学習データの数nとデータの変換gに対して不変な分布(学習対象のモデル)の次元K
に対して識別誤差確率が定められるというような定式化をされていて、
圧縮センシングと似ているというか関連があるらしいです。
データを点とするとそれへの群による作用の軌道を同一視するのを
random projectionで近似しているような感じなのでしょうか。
*2
Unsupervised learning of invariant representations
https://arxiv.org/pdf/1311.4158.pdf
という論文で詳細が語られているようです。
思ったこと
ここで紹介した論文では画像データの各箇所で同じ様な平行移動や回転を施すという大域的な変換のみが対象で局所的な変形は考慮されていません。群として扱うのは難しそうです。また輝度や色の変換に対する識別の頑健性、普遍性も重要ですが扱われてはいません。
*1:時系列などに対する畳み込みを考えれば自然なようです
*2:以前のrandom projection SVDに関する記事 http://xiangze.hatenablog.com/entry/2013/10/06/023524