stanによるニューケインジアン・フィリップス曲線の推定

経済学においては失業率とインフレ率をプロットすると負の相関関係が見られるというのが知られていてフィリップス曲線と呼ばれるそうです。
f:id:xiangze:20161002235530p:plain
https://gist.github.com/xiangze/b2a29f5f4ffb2be835b2#file-data_for_phillips-ipynb
その関係は10年程度の長期間では変化していき、原因として国ごとに様々な原因が考察されています。
各時点に対して失業率-インフレ率のプロットをして関係を見るのですが、各時点での値は独立ではなく、確率過程としてモデル化できると考えられます。実際ニューケインジアン・フィリップス曲線(NKPC)というモデル提唱されています。
実際のデータがどの程度当てはまるかを論文賃金版ニューケインジアン・フィリップス曲線に関する実証分析に沿ってstanで計算してみました。

データ

失業率 http://www.stat.go.jp/data/roudou/longtime/03roudou.htm#hyo_1 1953年から、2011年3~8月は補間値を用いている。
インフレ率(消費者物価指数) http://www.stat.go.jp/data/cpi/historic.htm
賃金上昇率(時間当たり賃金, 現金給与総額/総実労働時間　30人以上) http://www.e-stat.go.jp/SG1/estat/List.do?lid=000001139499

現金給与総額　季節調整済指数及び増減率（３０人以上）

のものを使いました。季節変動の補正はX12-ARIMAというARIMAアルゴリズムの実装を使っているそうです。https://ecitizen.jp/x-12-arima/
所得はボーナスがあるので季節により変動するのは予想できましたが、失業率や労働人口が季節変動するというのが個人的には意外でした。季節変動もベイズ推定する方が本当は良いのでしょうが、計算時間の関係で出来ませんでした*1。

モデル

賃金上昇率を用いたモデル(NKWPC)

論文の(17)の式です。
$\pi_t = \beta E_t[\pi_{t+1}]-\lambda \phi(u_t-u^n_n )$
$\pi_t$ : インフレ率,
$u_t$ :失業率,
$u^n_t$ : 自然失業率,
$\beta, \lambda, \phi$ : 係数
この式は元の論文では各時点での労働の需給を定常状態の近傍で線形化したもので
λは賃金の粘着性(変わりにくさ)が小さいときに大きくなりNKWPCの傾きは大きくなり、Φは"労働供給曲線の傾き"(失業率と賃金の間の係数)であり大きければNKWPCの傾きは大きくなります(論文9ページに図参照)。しかし式の上では一緒に出てきていてしまっていて上記式を前提とする限りは効果を分離できません。元論文でも一体化した値を推定しています(図表6)

元論文では時系列をローリング推定していますが、ここでは失業率と係数の時間発展にAR(2)モデルを使った以下のモデルで係数の推定を行いました。λΦ=Lとしています。

data{
  int<lower=1> N;
  real<lower=0,upper=100> pi[N];
  real<lower=0,upper=100> u[N];
}

parameters{
  real L[N]; //lambda*phi
  real<lower=0> un; //natural unemployment rate
  real<lower=-20,upper=20> beta[N];
  real uc[3];
  real cL[3];
  real b[3];
  real<lower=0> sb;
  real<lower=0> su;
  real<lower=0> sL;
  real<lower=0> s;
}

model{
  real p[N-1];

  for(i in 3:(N)){
             u[i]~normal(uc[1]+uc[2]*u[i-1]+uc[3]*u[i-2],su);
             L[i]~normal(cL[1]+cL[2]*L[i-1]+cL[3]*L[i-2],sL);
             beta[i]~normal(b[1]+b[2]*beta[i-1]+b[3]*beta[i-2],sb);
  }

  for(i in 1:(N-1))
             p[i]<-beta[i]*pi[i+1]-L[i]*(u[i]-un);

  for(i in 1:(N-1))
             pi[i]~normal(p[i],s);

  su~inv_gamma(0.0001,0.0001);
  s~inv_gamma(0.0001,0.0001);
  sL~inv_gamma(0.0001,0.0001);
  sb~inv_gamma(0.0001,0.0001);

}

NKPCmodels/model_fullstateAR2.stan at master · xiangze/NKPCmodels · GitHub
NKPC_AR.ipynb · GitHub

このモデルは収束し、自然失業率(固定)と係数L,βの時間変動の事後分布を得ることができました。
f:id:xiangze:20161003004825p:plain
自然失業率

f:id:xiangze:20161002040511p:plain
f:id:xiangze:20161002040505p:plain
Lとβ
f:id:xiangze:20161003010648p:plain f:id:xiangze:20161003010651p:plain
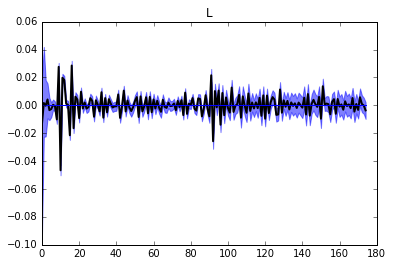
Lとβの25%～75%区間

係数Lはオイルショック(1974年ごろ)とバブル崩壊後(1994年ごろ)に大きく変動しています。賃金上昇率の時間変動の係数βはやはりバブル崩壊後に変動が大きくなっているように見えます。*2

インデグゼーションありモデル

交渉や契約によって賃金の上昇率にインフレ率が組み込まれているような場合にはインデグゼーションありモデル (論文の(21)) という以下のような物価上昇率に基づいた予測を取り入れたモデルが提唱されています。
$\pi_t = \alpha+\gamma\bar{\pi}_{t-1} +\beta E_t [\pi_{t+1} -\gamma \bar{\pi}^p_t ]-\lambda \phi(u_t-u^n_n )$
$\bar{\pi}^p _t$ : インデグゼーションによるインフレ率の指標

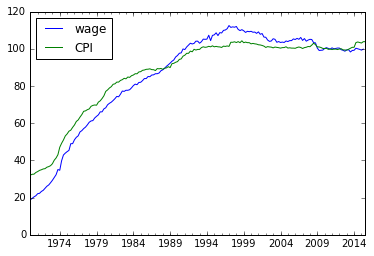
ここではCPIの上昇率を物価上昇率として用いました。CPIと賃金の相対的な関係は以下のようになっています。
f:id:xiangze:20161003004328p:plain

data{
  int<lower=1> N;
  real<lower=0,upper=100> pi[N];
  real<lower=0,upper=100> c[N];
  real<lower=0,upper=100> u[N];
}

parameters{
  real L[N]; //lambda*phi
  real<lower=0> un; //natural unemployment rate
  real alpha;
  real<lower=-20,upper=20> beta[N];
  real gamma[N];

  real uu[N];
  real cc[N];

  real uc[3];
  real cL[3];
  real b[3];
  real g[3];

  real<lower=0> su;
  real<lower=0> sL;
  real<lower=0> sb;
  real<lower=0> sg;
  real<lower=0> s;

  real<lower=0> soc;
  real<lower=0> sou;

}

model{
  real p[N];

  for(i in 3:(N)){
  u[i]~normal(uc[1]+uc[2]*u[i-1]+uc[3]*u[i-2],su);
  L[i]~normal(cL[1]+cL[2]*L[i-1]+cL[3]*L[i-2],sL);

  beta[i]~normal(b[1]+b[2]*beta[i-1]+b[3]*beta[i-2],sb);
  gamma[i]~normal(g[1]+g[2]*gamma[i-1]+g[3]*gamma[i-2],sg);
  }
  for(i in 1:(N)){
  u[i]~normal(uu[i],sou);
  c[i]~normal(cc[i],soc);
  }

  for(i in 2:(N-1))
  p[i]<-alpha+gamma[i]*cc[i-1]+beta[i-1]*pi[i+1]-L[i]*(uu[i]-un);

  for(i in 2:(N-1))
  pi[i]~normal(p[i]-gamma[i]*cc[i-1],s);
}

https://github.com/xiangze/NKPCmodels/blob/master/model_indegAR2.stan
NKPC_indeg.ipynb · GitHub

がこのモデルは収束しませんでした*3。
またこの式に失業率のARモデル
$u_t=\phi_0+\phi_1 u_{t-1} + \epsilon_t$
を逐次的に代入することでより簡単な
$\pi_t^w =\delta + \gamma \pi_{t-1}^p +\psi u_t$ 論文の式(22)
$\delta=\frac{1}{1-\beta} (\alpha+\lambda \phi (u^n - \frac{\beta \phi_0}{1-\beta \phi_1} ), \psi=\frac{\lambda \phi}{1-\beta \phi_1}$
というARモデルの形にできるのそうなのですが、この形に即したモデルでも係数δ、γが固定の場合、AR(2)の場合で収束しませんでした。
https://github.com/xiangze/NKPCmodels/blob/master/model_indeg_simpleAR2.stan