Persistent Homology とRのphom package, その他libraryの紹介

高次元データの大域的な性質に着目した分類、解析の手法にPersistent Homologyという方法があります。

またその手法を実装したRのパッケージ(CRAN phom package)があったので簡単に紹介いたします。その他の色々な言語で使えるライブラリについても最後に紹介いたします。

ホモロジーについて

ホモロジーとはあまり厳密でない言い方をすると微小な変形によっては変わることのないものの形状を特徴づけるような量で、一般には群の形で記述されます。群の係数としては整数や複素数などの数だけでなく、関数もとり得ます。しかしデータ解析の分野においては実係数のホモロジー群のみが対象とされる場合が多いようです。

球面、あるいはトーラス(ドーナツ型の図形)の表面は２次元ですが境目を持ちません。しかしながら全体としてみるとトーラスには穴が開いていて、球面には穴がありません。この穴に相当するものの有無、個数を表現するのがホモロジー群であるというのがざっくりした説明です。より高い次元においてもこのような図形を想像することができますが、直接見ることはできないためにやや遠回りで形式的な定義を用いる必要があります。

ホモロジーでは対象とする多次元図形の形をとらえるためにまず図形を局所的に簡単な要素に分割します。0次元図形の場合は点、1次元図形は線分、2次元図形の場合は3角形、3次元図形の場合は4面体がもっとも構成要素(点、辺、面)が少なく各次元の図形の一部分を占有することが出来ます。これを一般化した概念を単体と呼びます。

N次元空間内のN+1個の点の集合で、それらを結ぶことでN次元空間の一部分を占有できるようなものを単体(simplex)、複数の単体で、その一部を他の単体と共有しているものを単体的複体(Simplical Complex)と呼びます。

f:id:xiangze:20140329040829p:plain

単体の例

f:id:xiangze:20140329040836p:plain

単体的複体とそうでないものの例(http://www.coloquios.info/ponencias/MBGT-TopologicalDataAnalysis.pdf)

図形の単体的複体による分割によってその微妙な変形は単体の移動として扱えるので、単体的複体の構成要素には変化を与えません。

しかし分割法は一意ではなく、それだけでは図形の性質をとらえることは出来ません。

そこでr次元の各単体から生成される加群(係数が実数などの場合には各単体を基底とするようなベクトル空間)といったものを考えます。これを鎖複体(Chain Complex)

$C_r(K)=\{ \sum_i c_i \sigma_{r,i} | c_i \in K \}$

と呼びます(Kは係数の体,σ_rはr次元の単体)。

この鎖複体に対し境界作用素∂を用います。

∂はその名のとおり図形の境界を出力する演算子です。点p0,p0を結ぶ線分 $(p_0p_1)$ に対しては

$\partial (p_0p_1)=p_1-p_0$

となり、

各次元の鎖複体の間にも同様に境界作用素∂

[tex: \partial: C_q \rightarrow C_{q-1}]

が定義できます。

境界作用素を適用した場合に0になってしまうような鎖複体の集合を

f:id:xiangze:20140329212347p:plain

境界作用素の値域となる鎖複体の集合を

f:id:xiangze:20140329212358p:plain

とします。Z_r(K)のうちB_r(K)に含まれる鎖複体を同一視したもの

f:id:xiangze:20140329212410p:plain

をホモロジー群と呼びます。これは色々な単体的複体による図形の分割のうち自明な単体分割を同一視し、トーラスの穴の部分に引っかかるような分割の要素のみをとってくるような操作に相当します*1。

Persistent Homologyについて

以上が一般的なホモロジー群の概要ですが、Persistent Homologyでは単体的複体の代わりにVietoris-Rips Complex, またはCech complexと呼ばれるもののホモロジー群を計算することになります(以下の図はBarcodes: The Persistent Topology of Dataからの引用です)。

これはデータの点群(Point Cloud)に対して定義されるものであり、下図のようにある点と一定距離内にある点とを線で結び単体的複体を構成していく方法です。距離のパラメータεが小さい場合はほとんどの点は連結せず、一定以上大きくすると次第に連結していきます。ノイズに起因するむらなどで小さな穴があり、εをさらに大きくしていくと穴は埋まっていき最後には1つの塊となってしまいます。

f:id:xiangze:20140329040914p:plain

点から一定距離の範囲(赤丸)と点を結んでできた単体(青)

f:id:xiangze:20140329041016p:plain

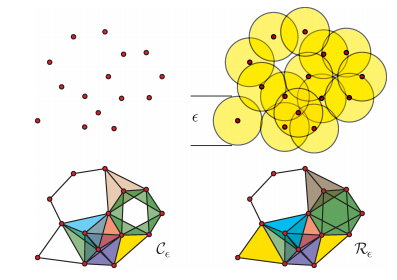
距離パラメータεを固定した場合のCech Complex(C_e)とVietoris-Rips Complex

f:id:xiangze:20140329041026p:plain

距離パラメータεを大きくしていった場合に単体的複体が密になっていき、穴が埋まっていく様子

距離パラメータεの異なるVietoris–Rips Complexで計算したホモロジー群の次元(betti数)を連結成分ごとにヒストグラム化し、プロットしたものをbarcodeと呼びます。

これによってデータの形状の分類、比較をするのがpersistent homologyの手法のようです。

f:id:xiangze:20140329041037p:plain

各εでのVietoris–Rips Complex(上図)とbarcode(下図) 点線はεの値に対応している。

上の図ではεが小さいうちは連結成分の数に対応するH0はばらけており、εが大きくなると連結成分は集約され、穴があいた状態になり、H1の要素が出てきます。さらにεを大きくするとH2が出現しますが、直ぐに埋まってしまい、H1も埋まってしまい、消滅してしまいます。この穴のパラメータεに対する存続する具合のことをPersistenceとよび、Persistent Homologyの用語の由来となっています。長く存続していて出現位置がかぶっているbarの数がそのデータ集合のbetti数ということになります。

このような点を結ぶグラフでデータの集合をとらえようとする方法として多様体学習の手法の中でもIsomapがよく知られています。Isomapでは作成されるグラフが低次元に収まるように適切な数の近傍点をとる必要がありましたが、persistent homologyでは全ての距離パラメータεに対して近傍に相当する点を結んだグラフを作成し、単体的複体としてbetti数を計算しなければいけないのでかなり計算量は多くなってしまいます。

CRAN phom package

２つの計算方法をとることが出来て

• Vietoris-Rips mode(素朴な方法？)

• Lazy-Witness mode(遅延的に計算することで計算を高速化？)

入力としては

• Euclidean Data(通常の行ごとのデータ)

• Distance Matrix

に対応しているようです。

Barcode plotは横軸各解像度に対する非連結成分のヒストグラムになります。

もっとも細かい解像度ではヒストグラムのビンの数はデータ点と同じになってしまい、傾向が掴みづらい場合があります。そのためPersistence Diagramという散布図も用意されています。

Persistence DiagramはBarcodeの各binの始まりのεと終わりのεが2次元座標の組みとしてプロットされたものです。各次元での値に対応する散布点が色別に表示されます。

例

vignetteの例です。

2次元混合ガウス分布

f:id:xiangze:20140329041111p:plain

f:id:xiangze:20140329041200p:plain

Barcode plot

最後(右側)の方でbarが2本だけになってしばらくしてから１本になるところでクラスターが2つあることが判別できます。

S^3={x^2+y^2+z^2+w^2=1}

f:id:xiangze:20140329041142p:plain

Persistence Diagram

H0とH3ではそれぞれ１個の点のInterval Endが大きく、H1,H2では小さく b0=1,b1=0,b2=0 b3=1を示唆しています。これは一般的な球のホモロジー群の計算の結果と一致します。

上記の例はほとんど自明なのでもっと面白い例示がしたいです。

続く

Libraries

phom R BSD

PLEX Matlab

PHAT(Persistent Homology Algorithm Toolbox) c++, LGPL

Dionysus c++,Python バインディングがあります。GPL

javaplex Javeで書かれています。BSD

Perseus c++, discrete Morse theoryに基づく

CHomP(GitHub) c++ 下記の本で紹介されています。

Persistent Homologyは元々コンピュータビジョンの分野で提唱されたようですが、現在では純粋数学の分野での研究のほうが盛んなようです。点群を扱うライブラリとして有名なPCL(Point Cloud Library)の中にも実装はされていないようです。上記ライブラリと組み合わせて使うことが出来るかもしれません。